Стеганография. Скрытие информации в изображениях
Автор: kost![kost [ @ hackerdom ] . ru](./pictures/kost_mail.gif)
Введение
В этой статье я постараюсь сделать небольшой экскурс в историю развития стеганографии, осветить основные ее аспекты, особенно подробно остановлюсь на скрытии информации в изображениях, приведу пример простейшей программы, которая прячет данные в изображениях формата .bmp, разберу идею формата .jpeg и укажу место, где в нем возможно спрятать информацию. И, наконец, упомяну пару забавных простеньких примеров скрытия данных на вашем домашнем компьютере, о которых не все знают.
Идеология
В настоящее время, проблема обеспечения конфиденциальности хранимых и, особенно, пересылаемых данных стала чрезвычайно острой. Первая мысль, которая приходит, когда начинаешь думать о закрытости данных – это шифрование. То есть представление данных в таком виде, в котором, не зная ключа, их невозможно было бы понять. Эти данные можно более или менее безопасно хранить и пересылать по общедоступным каналам связи. Такой способ защиты информации, называемый криптографической защитой (криптографией), широко используется как в компьютерной, так и в других сферах жизни человеческого общества. Цель криптографии состоит в блокировании несанкционированного доступа к информации путем шифрования содержания секретных сообщений. Мы же поговорим о другом варианте обеспечения конфиденциальности данных – о стеганографической защите (стеганографии).
Идея стеганографии состоит в том, чтобы скрыть сам факт сокрытия какой-либо информации. При этом оба способа можно объединить и использовать вместе, для повышения эффективности защиты информации (например, при передаче криптографических ключей).
Прах времен
Методы стеганографии можно проследить с древних времен. Например, в Древней Греции для письма служили деревянные дощечки, покрытые сверху воском. И использовали иногда такое ухищрение: соскабливали воск с дощечки – выскребывали послание на дереве – а потом вновь наносили сверху воск. Ну и, например, уже на воске можно было выскрести какое-нибудь ложное (fake) послание. Или ничего не выскребать – таблички бы выглядели чистыми и не вызывали бы подозрений.
Хорошо известны различные способы скрытого письма между строк обычного, не защищаемого текста: от применения молока (Россия знает об этом способе по ухищрениям дедушки Ленина ;) ) до использования сложных химических реакций с последующей обработкой для прочтения.
Другие методы стеганографии включают использование микрофотоснимков, незначительные различия в написании рукописных символов, маленькие проколы определенных напечатанных символов и множество других способов по скрытию истинного смысла тайного сообщения в открытой переписке.
Вспомним еще раз про передачу посланий с использованием постороннего текста (книги, газетной статьи, письма, …). И здесь простор для фантазии просто огромен: скрытый текст может считываться по первым буквам слов (принцип акростиха) или определяться по заранее оговоренному правилу. После изобретения общепринятых кодов (например, азбуки Морзе) стало возможным распознавать секретный текст по длинам слов. Например: 4-5 букв — тире, 5-6 букв — точка, 7 и более — пробел, менее 4 букв — игнорируются.
Ну, а собственно причиной, по которой статья посвящена именно компьютерной стеганографии, является появление и бурное развитие computer science в последние полвека. И именно компьютерная техника раскрывает все возможности, всю неисчерпаемую глубину и интересность этой проблемы. То, о чем во Вторую Мировую войну мечтали воюющие стороны, стало обыденной реальностью сейчас. Современный прогресс в области глобальных компьютерных сетей и средств мультимедиа привел к разработке новых методов, предназначенных для обеспечения безопасности передачи данных по каналам телекоммуникаций и использования их в необъявленных целях. Эти методы, учитывая естественные неточности устройств оцифровки и избыточность аналогового видео или аудио сигнала, позволяют скрывать сообщения в компьютерных файлах (контейнерах). Причем, в отличие от криптографии, данные методы скрывают сам факт передачи информации.
Формальности
Я приведу основные понятия стеганографии, с которыми столкнулся на просторах Интернета, когда готовился к докладу на семинаре Хакердом в УрГУ осенью 2006 г. Сразу скажу, что я здесь не буду останавливаться на прочих понятиях и абстракциях (типа файл, формат, мультимедиа, алгоритм, байт, …). В современной компьютерной стеганографии существует два основных типа файлов: сообщение — файл, который предназначен для скрытия, и контейнер — файл, который может быть использован для скрытия в нем сообщения. При этом контейнеры бывают двух типов. Контейнер-оригинал (или “Пустой” контейнер) — это контейнер, который не содержит скрытой информации. Контейнер-результат (или “Заполненный” контейнер) — это контейнер, который содержит скрытую информацию. Под ключом понимается секретный элемент, который определяет порядок (алгоритм) занесения сообщения в контейнер. Направления развития стеганографии следующие:
- Методы, основанные на использовании специальных свойств компьютерных форматов;
- Методы, основанные на избыточности аудио и визуальной информации.
Сейчас, наверное, стоит наконец-то приостановить поток вываливаемой на читателя теории – ибо она может показаться скучной и не относящейся к делу. Приведем же наконец-то практический пример (он касается первого направления):
Маленькие шалости
Очень распространены 2 следующих формата: rar и jpeg. В первом хранятся заархивированные данные. Второй используется для хранения данных, сжатых по алгоритму сжатия изображений jpeg. Если внимательно приглядеться к их внутреннему устройству (я не буду здесь приводить точную спецификацию), то можно заметить, что в самое начало файла можно вставить практически любую информацию – она будет игнорироваться программами-архиваторами (winrar, к примеру) – так как они пропускают все до тех пор, пока не натолкнутся на определенную метку. То есть если сообщение не содержит такой метки в качестве какой-либо своей подпоследовательности, то коллизий не возникнет. Ну, а формат jpeg предусматривает хранение длины файла, и из-за этого программы для просмотра изображений игнорируют какое-либо сообщение, вставленное в конец файла. В связи с этим представляется любопытным провести следующий эксперимент:
Попробовать взять какое-нибудь изображения в формате jpeg и дописать в конец него rar-архив. Мы увидим, что все действительно работает так, как нам хотелось бы – при просмотре файла, например с помощью ACDSee, нам открывается наше изображение. А при попытке его разархивировать – все тоже проходит гладко, и мы спокойно себе получаем наше сообщение. Естественно можно на архив наложить шифрование – и получить таким образом «спайку» возможностей криптографии и стеганографии.
Скажем сразу и о втором нехитром способе утаить что-нибудь от не слишком пытливого взгляда на своем компьютере. А именно: хранить скрываемые данные в альтернативных потоках файловой системы NTFS. Любопытно то, что стандартные средства Windows (типа Проводника) не позволяют выявить наличие информации в этих потоках. Даже на показываемом размере файла не сказывается наличие информации в альтернативном потоке. К сожалению, этот способ не всегда пригоден при пересылке данных, ибо он основан на особенностях файловой системы NTFS (правда, уже упомянутый выше winrar умеет сохранять альтернативные потоки). А редактировать потоки можно хоть в том же Блокноте Windows (если это текст) – нужно лишь знать имя потока – и набрать в cmd примерно следующее:
Еще раз повторю, что это далеко не единственный способ. Кроме того, в зависимости от настроек Windows, версии, у вас может получиться, а может и нет этот фокус с потоками (через блокнот). При попытке скопировать такой файл на устройство с файловой системой, не поддерживающей потоки (например, на флеш-диск) или же по сети (не берусь утверждать ничего про различные протоколы, но вот с SMB я проверял) – вам высветится сообщение о том, что информация в сопутствующих потоках может быть потеряна. Кстати, таким образом можно узнать, содержит ли такие потоки, и если да, то какие, подозрительный файл.
Шаманим с BMP
Выше было упомянуто и второе направление стеганографии, а именно: методы, основанные на избыточности аудио и визуальной информации . Поговорим сейчас о них. В сети можно найти массу подсчетов, сколько информации можно "дополнительно" сохранить в данном изображении/видео/звуковом файле… Давайте немного осветим вопрос о способах хранения этих данных в цифровом виде. Представляется очевидным, что в компьютерах все конечно и дискретно. В связи с этим мы храним лишь отдельные части изображений/звуков/… В простейшем варианте (формат bmp = bitmap picture) изображение хранится как матрица (таблица) значений оттенков цвета для каждой точки хранимого изображения. Это означает, что изображение разбивается на прямоугольник из точек и для каждой точки хранится ее цвет. Ну и, разумеется, он хранится не как длина его волны (вспоминаем немного физику), а как комбинация из трех оттенков (красного, зеленого и синего цветов - это называется схема смешения RGB) которые необходимо "смешать" для того чтоб получить наш исходный цвет. Сразу следует оговориться, что здесь и далее я буду иметь в виду ту часть формата bmp, которая предусматривает хранение трех байт на каждый пиксель изображения (то есть не рассматриваются такие, безусловно, важные и востребованные вещи, как прозрачность, палитры цветов и прочее). Таким образом, каждая из трех компонент (их еще называют каналами цвета), хранясь в одном байте, может принимать значения от 0 до 255 включительно. Особенность нашего зрения заключается в том, что мы достаточно терпимо относимся к незначительным колебаниям цвета. Это значит, что мы не заметим разницы между цветами, соответствующими значениям, отстоящим друг от друга в пределах 3. Например, 140 и 142. Разумеется, у разных людей эта допустимая погрешность будет варьироваться, но соседние значения (скажем, 120 и 121) вряд ли кто-либо сможет различить. Изменение каждого из трех наименее значимых бит (в трех каналах соответственно) приводит к изменению менее чем на 1% интенсивности данной точки. А это, в свою очередь означает, что наименее значащий бит (тут от читателя потребуется понятие о двоичной арифметике и представлении целых чисел в компьютере) мы можем изменять по своему усмотрению. Это называется принцип "наименее значащих битов" = Least Significant Bits. Если отбросить в расчетах, обычно незначительную относительно размера изображения, служебную информацию в начале файла, то получаем следующую картину. Мы имеем возможность дополнительно хранить сообщение размером в 1/8 размера контейнера ("размазанную" по последним битам в каждом байте матрицы цветов пикселей) или же размером в 1/4 контейнера (соответственно при использовании 2 последних битов в байтах). Это, согласитесь, немало. Мною была написана на С++ простенькая программа, реализующая эту идею. Она предназначена лишь для демонстрации и далеко не идеальна (к примеру, информация о размере сообщения хранится в зарезервированных разработчиками стандарта байтах – что приводит к невозможности извлечения сообщения обратно после банального просмотра изображения и сохранения его (не внося изменений), так как графические редакторы заполняют, согласно стандарту, нулями эти поля). Исходники (под Visual Studio 6) прилагаются.
Аццкий JPEG
Все это было бы хорошо, если б не столь малая распространенность этого формата при передачи изображений по сети. Связано это с тем, что в изображениях, вообще говоря, много избыточности и поэтому они хорошо ужимаются, особенно алгоритмами архивации с потерями. Наиболее распространен в данный момент формат JPEG (Joint Photographic Experts Group). Здесь уже не получится такой фокус, так как этот формат намного более сложный, нежели bmp. В нем применяются специальные алгоритмы преобразования цветовых пространств, архивации, квантования. Но обо всем по порядку.
- Вообще мы будем работать не со всем изображением сразу, а с его частями – кусочками 8x8 пикселей. То есть для начала разбиваем исходное изображение на такие подизображения, как изображено на рисунке 1 (Здесь и далее иллюстрации взяты с wikipedia.org).

Рис. 1. Кусочки изображения 8x8 пикселей - Преобразование цветового пространства: [R G B] -> [Y Cb Cr] (R,G,B - 8-битовые величины без знака)
| Y | | 0.299 0.587 0.114 | | R | | 0 | | Cb | = | -0.1687 -0.3313 0.5 | * | G | + |128| | Cr | | 0.5 -0.4187 -0.0813 | | B | |128|
(от читателя требуется представление о перемножении матриц)
Новая величина Y = 0.299*R + 0.587*G + 0.114*B названа яркостью. Это – величина, используемая монохромными мониторами, чтобы представить цвет RGB. Физиологически, передает интенсивность цвета RGB, воспринятого глазом. Видно, что формула для Y похожа на средневзвешенное значение с разным весом для каждого спектрального компонента: глаз наиболее чувствителен к зеленому цвету (G), затем следует красный (R) компонент и в последнюю очередь – синий (B).
ВеличиныCb = - 0.1687*R - 0.3313*G + 0.5 *B + 128 и Cr = 0.5 *R - 0.4187*G - 0.0813*B + 128
названы цветовыми величинами и представляют 2 координаты в системе, которая измеряет оттенок и насыщение цвета ([Приближенно] эти величины указывают количество синего и красного в этом цвете). Эти 2 координаты кратко названы цветоразностью.
Глаз, особенно сетчатка, имеет как визуальные анализаторы два типа ячеек: ячейки для ночного видения, воспринимающие только оттенки серого (от ярко-белого до темно-черного) и ячейки дневного видения, которые воспринимают цветовой оттенок. Первые ячейки (их называют палочками), обнаруживают уровень яркости, подобный величине Y. Другие ячейки(их называют колбочками), ответственные за восприятие цветового оттенка, - определяют величину, связанную с цветоразностью. Они, соответственно бывают 3-х видов – воспринимающие лучше красный, зеленый и синий цвета.
- Дискретизация.
Кроме всего прочего, глаз более чувствителен к яркости света, нежели чем к оттенку. Поэтому разумно брать значение яркости для каждого пикселя. А значения цветоразности – например среднее для блока 2x2. То есть на каждые 4 пикселя одно. Разумеется, это необязательно, но почти всегда применяется, так как ведет к незначительным потерям качества с точки зрения восприятия картины глазом человека.
- Сдвиг уровня
Все 8-битовые величины без знака (Y,Cb,Cr) в изображении - "смещенные по уровню": они преобразовываются в 8-битовое знаковое представление вычитанием 128 из их величины. Возьмем некоторый пример. Пусть у нас есть такая матрица (рис. 2), описывающая одну из компонент Y, Cb или Cr.
После сдвига уровня соответственно: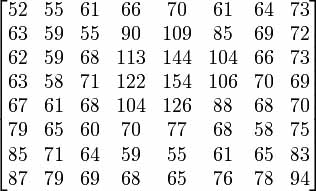
Рис. 2. Матрица описывающая одну из компонент Y, Cb или Cr.
Рис. 3. После сдвига уровня. - 8x8 Дискретное Косинусоидальное (Косинусное) Преобразование (DCT)
Цель DCT-трансформации в том, что вместо обработки исходных изображений, Вы работаете с пространством частот изменения яркости и оттенка. Эти частоты очень связаны с уровнем детализации изображения. Высокие частоты соответствуют высокому уровню детализации. Я не буду вдаваться в детали – они потребуют много знаний из области высшей математики, да и займут много скучного места. Коротко объяснить суть не получится – просто поверьте, что все так, как написано. Скажу лишь, что DCT-трансформация очень похожа на 2-мерное преобразование Фурье, которое получает из временного интервала (исходный блок 8x8) частотный интервал (новые коэффициенты 8x8=64, которые представляют амплитуды проанализированного частотного пространства).
После этого преобразования мы получим другую матрицу – и в ней уже элементы будут так расположены, что наибольшие по модулю скопятся в левом верхнем углу – они будут нести в себе бОльшую часть информации – низкие частоты. А по мере продвижения к правому нижнему – важность элементов будет уменьшаться – высокие частоты.

Рис. 4. без названия - Квантование
Именно на этом этапе мы и терпим почти все потери – но именно этот этап и дает нам возможность затем так хорошо сжать информацию. По определенной заранее матрице квантования происходит деление элементов нашей матрицы соответственно на элементы матрицы квантования. Она имеет следующий вид:
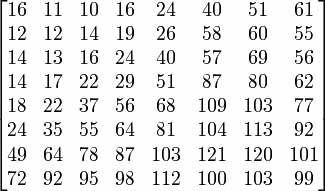
Рис. 5. Матрица квантованияЭта матрица квантования опирается на "психовизуальный порог". Обычно присутствует одна таблица для Y, и другие для оттенка Cb и Cr. Здесь происходит удаление высоких частот, мы это делаем потому, что глаз более чувствителен к низким частотам. Это происходит при делении тех элементов матрицы, что находятся ближе к правому нижнему углу (они отвечают за высокие частоты) на бОльшие, а тех, что в левом верхнем углу - на меньшие значения. Больше величины в таблице квантования - больше потери (впоследствии визуальные потери) введенные этим процессом, и меньше – лучше визуальное качество.
В результате этой операции в правом нижнем углу скопится много нулей, как изображено на следующем рисунке.

Рис. 6. Результат деления на матрицу квантования - Зигзаг-сканирование
Преобразуем матрицу 8x8 в вектор из 64-х элементов следующим образом:
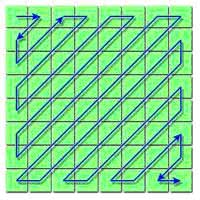
Рис. 7. Зигзаг-сканированиеПосле того, как мы прошли по зигзагу матрицу 8x8, мы имеем теперь вектор с 64 коэффициентами (0..63) Смысл этого зигзагообразного вектора – в том, что мы просматриваем коэффициенты в порядке повышения пространственных частот. Так мы получаем вектор, отсортированный критериями пространственной частоты.
- RLE – сжатие.
На данный момент у нас есть вектор с большим количеством подряд идущих нулей в старших коэффициентах. Известно, что выгоднее просто записать вместо этого сначала некоторую метку, а потом только количество этих одинаковых байтов (в нашем случае не нужно конкретизировать какой именно байт – так как заранее известно, что это 0) Например, вместо -1,1,-1,2,0,0,0,0,0,0 можно написать: -1,1,-1,2,[escape-символ],6
- Кодирование Хаффмана
Наконец, полученное сжимается по Хаффману (RLE и сжатие по Хаффману - алгоритмы сжатия без потерь). Я не буду вообще останавливаться на этом месте – в Интернете на эту тему можно массу всего найти. Ну а итог уже записывается в файл вместе с заголовком, определяющим различные параметры, длину изображения и прочее, и прочее…
Финал-апофеоз водобачкового инструмента
Теперь вспомним, что тема этой статьи все же стеганография – то есть скрытие информации и попытаемся понять – куда же тут можно встроиться? Понятно, что бесполезно встраивать информацию до квантования – так как оно осуществляет те самые потери, которых нам нужно избежать – ведь сообщение должно быть передано без искажений! Также представляется очевидным, что нельзя изменять данные, уже в сжатой форме – ведь разжатие может оказаться непредсказуемым. Казалось бы, остается только изменение данных непосредственно перед RLE-кодированием – что может привести к сильным потерям – ведь там уже не просто компоненты смешения RGB как было в bmp, либо ухудшению качества сжатия – если некоторые нули превращать, скажем, в единицы – разбивая тем самым последовательности нулей на части.
Я же предлагаю воспользоваться предоставляемой возможностью из-за ограничений, накладываемых алгоритмом Хаффмана, сжать одну и ту же информацию при помощи RLE разными вариантами. Дело в том, что на самом деле в JPEG используется несколько другая форма сжатия RLE. Допустим, мы имеем 57,45,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,23,0,30,0,0,0,0,0,0,…,0 (Здесь между 45 и 23 идет 17 нулей)
Для этого примера сжатие будет выглядеть вот так:
(0,57); (0,45); (17,23); (1,30); [маркер]
Как видите, мы кодируем для каждой величины количество последовательных ПРЕДШЕСТВУЮЩИХ нулей перед величиной, затем мы добавляем величину. А маркер символизирует, что оставшиеся до конца числа – нули. Ну а сжатие Хаффмана накладывает такое ограничение: число предшествующих нулей должно кодироваться как 4-битовая величина - не может превысить 15.
Так, предшествующий пример должен быть закодирован как:
(0,57); (0,45); (15,0); (1,23); (1,30) (забудем сейчас про маркер - нам он сейчас не важен)
(0,57); (0,45); (14,0); (2,23); (1,30) или (0,57); (0,45); (13,0); (3,23); (1,30)
Вот эту неоднозначность я и предлагаю использовать для скрытия. Простейшая мысль, которая приходит в голову. Помещая очередной бит сообщения, при встрече подобной неоднозначности, если мы хотим поместить 0, то оставляем …, (15,0), (2,3), … если хотим 1 – то "перетаскиваем" единичку в следующий элемент (если это возможно – ведь там может оказаться тоже (15,0)).
Проблема, которая видна при реализации такой идеи – нет уверенности, что все программы для просмотра jpeg формата способны правильно интерпретировать такую замену – возможно в них существует проверка, что если идут подряд 2 таких элемента, описывающих подряд идущие нули – то в первом должно быть всегда 15. Но это требует всего лишь проверки. Что я и предлагаю вам осуществить.
На эту тему можно писать еще долго, очень интересны вопросы применения нейросетей в стеганографии и многое другое, но эта статья заканчивается, всем дочитавшим спасибо и удачи! Рад буду всем отзывам и предложениям.